generate

It generates a multivarite random series according to the model x

generate(x = NULL, ...)

# Default S3 method
generate(
  x,
  FUN = rnorm,
  n = 100,
  K = 3,
  names = NULL,
  cov = NULL,
  gap.filling = NULL,
  ...
)

# S3 method for class 'varest'
generate(
  x,
  FUN = rnorm,
  n = 100,
  names = NULL,
  noise = NULL,
  exogen = NULL,
  xprev = NULL,
  gap.filling = NULL,
  ...
)

# S3 method for class 'varest2'
generate(
  x,
  FUN = rnorm,
  n = 100,
  names = NULL,
  noise = NULL,
  exogen = NULL,
  xprev = NULL,
  gap.filling = NULL,
  ...
)

# S3 method for class 'GPCAvarest2'
generate(
  x,
  FUN = rnorm,
  n = 100,
  names = NULL,
  noise = NULL,
  exogen = NULL,
  xprev = NULL,
  extremes = TRUE,
  type = 3,
  gap.filling = NULL,
  GPCA.row.gap.filling.option = TRUE,
  ...
)

# S3 method for class 'matrix'
generate(
  x,
  FUN = rnorm,
  n = 100,
  noise = NULL,
  xprev = NULL,
  names = NULL,
  gap.filling = NULL,
  type = c("autoregression", "covariance"),
  ...
)

# S3 method for class 'list'
generate(x, factor.series = names(x), n = NA, ...)

# S3 method for class 'MonthlyList'
generate(x, origin, n, ...)

Arguments

x: null object or the model used for random generation , e.g. a VAR model as a varest-class or varest2-class object. Default is NULL.
...: further arguments for FUN
FUN: random function of the probability distribution used for noise random generation. Default is rnorm. See https://CRAN.R-project.org/view=Distributions
n: number of generations requested
K: number of the variables to be generated simultaneously, i.e. the K parameters of a VAR. It is automatically detected by x, names or cov, if one of these is not NULL.
names: null object or string vectors or names of the variables to be generated simultaneously. Default is NULL.
cov: null object or covariance matrix of the random variables to be generated simultaneously. Default is NULL, not used in case this information can be detected from x.
gap.filling: data frame with time series with gabs (NA values) to be filled. Default is NULL and not considered, otherwise the method returns this data frame with NA row replaced with generated (e.g auto-regressed) values.
noise: null object or a generic external noise for x model residuals, e.g. standard white noise, for random generation with the model x. Default is NULL. If NULL the noise is automatically calculated.
exogen: null object or amatrix or data frame with exogeneous variables (predictors) id requested by x. Default is NULL
xprev: null object or initial condition of the multivariate random process to be generated. Default is NULL.
extremes: see inv_GPCA
type: character string used in some method implementations. See inv_GPCA. In the matrix implementation, default is "autoregression", i.e. the matrix is used as a vector auto-regression coefficient, if it is "covariance" the method genereted a sample with covariance matrix given by x.
GPCA.row.gap.filling.option: logical value. Default is TRUE. In case of GPCAvarest2-class objects, If gap.filling contains both NA and finite values in the same row, this row will contains all NA values after GPCA. In this case all row values are generated through auto-regression. If GPCA.row.gap.filling.option all insterted non-NA gap.filling values are repleced before returning the function value. Otherwise, in the rows with NAs all values are re-generated. The option TRUE is not safe in case the gaps are vary long becouse the genereted values is used for subsequent auto-regrossion.
factor.series: factor series used by 'factor.series'
origin: start date for generation. See adddate

Value

a matrix or a data frame object

Examples





library(RGENERATE)

set.seed(122)
NSTEP <- 1000
x <- rnorm(NSTEP)
y <- x+rnorm(NSTEP)
z <- c(rnorm(1),y[-1]+rnorm(NSTEP-1))
df <- data.frame(x=x,y=y,z=z)
var <- VAR(df,type="none")
gg <- generate(var,n=20) 

cov <- cov(gg)

ggg <- generate(FUN=rnorm,n=NSTEP,cov=cov)

 
library(RMAWGEN)
exogen <- as.data.frame(x+5)
gpcavar <- getVARmodel(data=df,suffix=NULL,p=3,n_GPCA_iteration=5,
n_GPCA_iteration_residuals=5,exogen=exogen)
#> Warning: No column names supplied in exogen, using: exo1 , instead.
gpcagg <- generate(gpcavar,n=20,exogen=exogen) 

## Generate an auto-regrassive time-series with a generic matrix 

A <- diag(c(1,-1,1))
mgg <- generate(A,n=100)

### Gap Filling Examples

 dfobs <- df
 dfobs[20:30,] <- NA 
 n <- nrow(df)
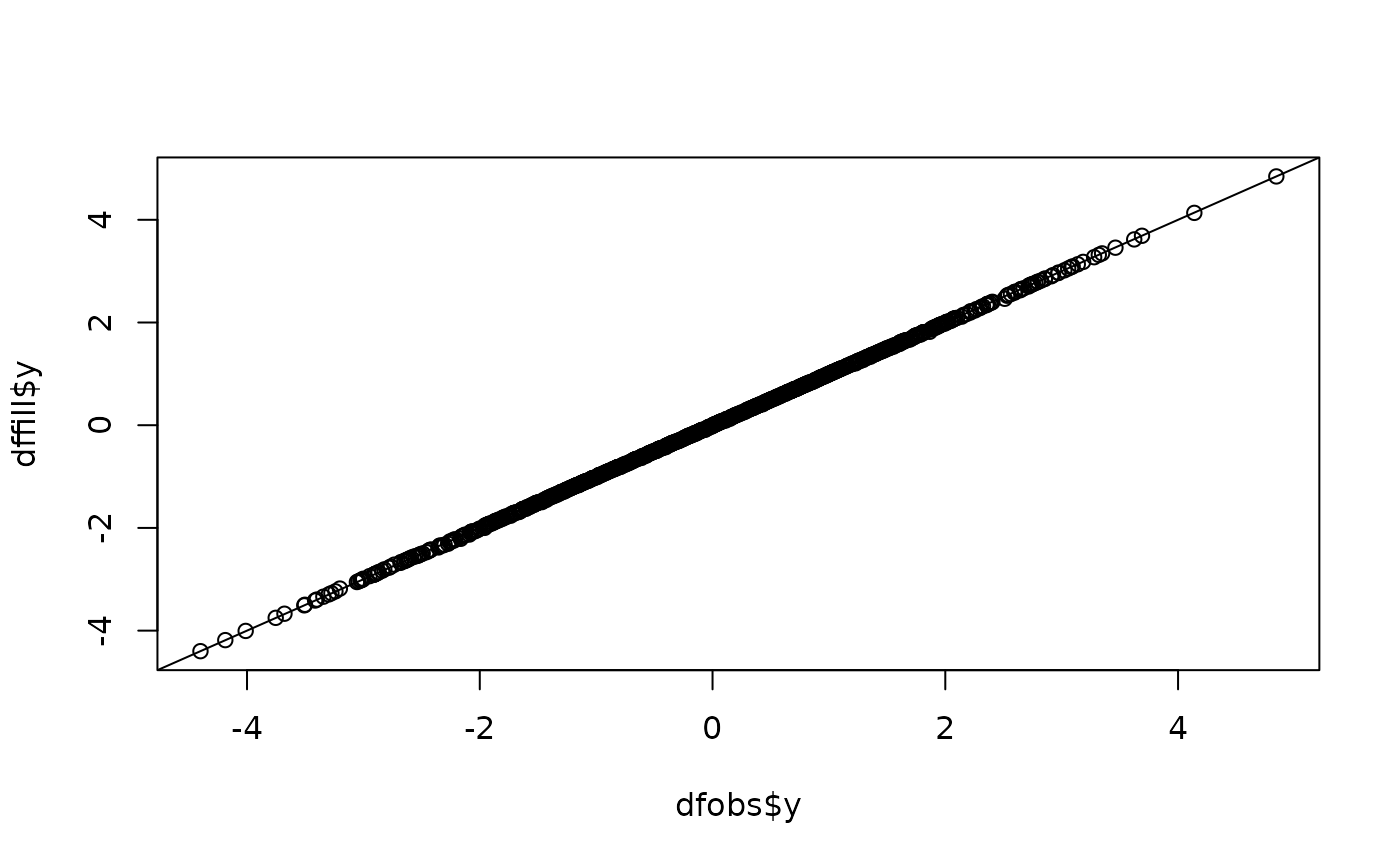
 dffill <- generate(gpcavar,n=n,exogen=exogen,gap.filling=dfobs,names=names(dfobs)) 
 
qqplot(dfobs$y,dffill$y)
abline(0,1)


### Gap filling with matrix 

mgg_n <- mgg
mgg_n[20:30,2] <- NA 

mgg_nfill <- generate(A,gap.filling=mgg_n)

print(mgg_n[1:31,])
#>            V1         V2         V3
#> 1  -0.2470608  0.0000000  -2.141684
#> 2  -2.5283796  2.7929754  -2.751822
#> 3  -0.9404160 -3.7057097  -4.217328
#> 4  -2.1996566  4.5960217  -2.287199
#> 5  -1.6667400 -3.1899526  -2.665821
#> 6  -2.5333364  3.7210993  -2.730603
#> 7  -2.3018206 -3.2843622  -3.121786
#> 8  -4.5278923  2.7796531  -4.311586
#> 9  -2.9008246 -2.3305299  -6.562964
#> 10 -4.0334442  2.1737427  -6.520765
#> 11 -3.1696797 -3.3890267  -7.119447
#> 12 -3.1716013  2.3790693  -7.720275
#> 13 -3.5124602 -1.5798547  -5.870427
#> 14 -4.1098562  1.2031298  -6.337695
#> 15 -3.3570146  0.1027575  -7.599490
#> 16 -3.0143610 -1.4631478  -7.019519
#> 17 -2.4977306  1.2944133  -7.691805
#> 18 -2.6130060 -1.2606028  -8.579758
#> 19 -3.4743921  2.3126528  -8.271425
#> 20 -3.0145004         NA  -9.043722
#> 21 -3.6072536         NA -10.524975
#> 22 -4.3188987         NA -10.317646
#> 23 -2.7552194         NA  -9.549761
#> 24 -3.2948209         NA -10.454133
#> 25 -3.6228292         NA -11.380552
#> 26 -3.6630571         NA -13.035626
#> 27 -4.7831600         NA -12.115321
#> 28 -5.8326471         NA -11.135454
#> 29 -4.9125059         NA -12.490254
#> 30 -4.1017955         NA -14.407694
#> 31 -3.8445887 -1.0739763 -14.368059
print(mgg_nfill[1:31,])
#>            V1         V2         V3
#> 1  -0.2470608  0.0000000  -2.141684
#> 2  -2.5283796  2.7929754  -2.751822
#> 3  -0.9404160 -3.7057097  -4.217328
#> 4  -2.1996566  4.5960217  -2.287199
#> 5  -1.6667400 -3.1899526  -2.665821
#> 6  -2.5333364  3.7210993  -2.730603
#> 7  -2.3018206 -3.2843622  -3.121786
#> 8  -4.5278923  2.7796531  -4.311586
#> 9  -2.9008246 -2.3305299  -6.562964
#> 10 -4.0334442  2.1737427  -6.520765
#> 11 -3.1696797 -3.3890267  -7.119447
#> 12 -3.1716013  2.3790693  -7.720275
#> 13 -3.5124602 -1.5798547  -5.870427
#> 14 -4.1098562  1.2031298  -6.337695
#> 15 -3.3570146  0.1027575  -7.599490
#> 16 -3.0143610 -1.4631478  -7.019519
#> 17 -2.4977306  1.2944133  -7.691805
#> 18 -2.6130060 -1.2606028  -8.579758
#> 19 -3.4743921  2.3126528  -8.271425
#> 20 -3.0145004 -1.7122995  -9.043722
#> 21 -3.6072536  1.0642612 -10.524975
#> 22 -4.3188987 -1.9391198 -10.317646
#> 23 -2.7552194  1.9041245  -9.549761
#> 24 -3.2948209 -1.1833081 -10.454133
#> 25 -3.6228292  2.7985222 -11.380552
#> 26 -3.6630571 -4.0100472 -13.035626
#> 27 -4.7831600  1.7256381 -12.115321
#> 28 -5.8326471 -3.2995169 -11.135454
#> 29 -4.9125059  2.3226831 -12.490254
#> 30 -4.1017955 -1.5975275 -14.407694
#> 31 -3.8445887 -1.0739763 -14.368059

dfobs2 <- df
dfobs2[20:30,2] <- NA
n <- nrow(df)
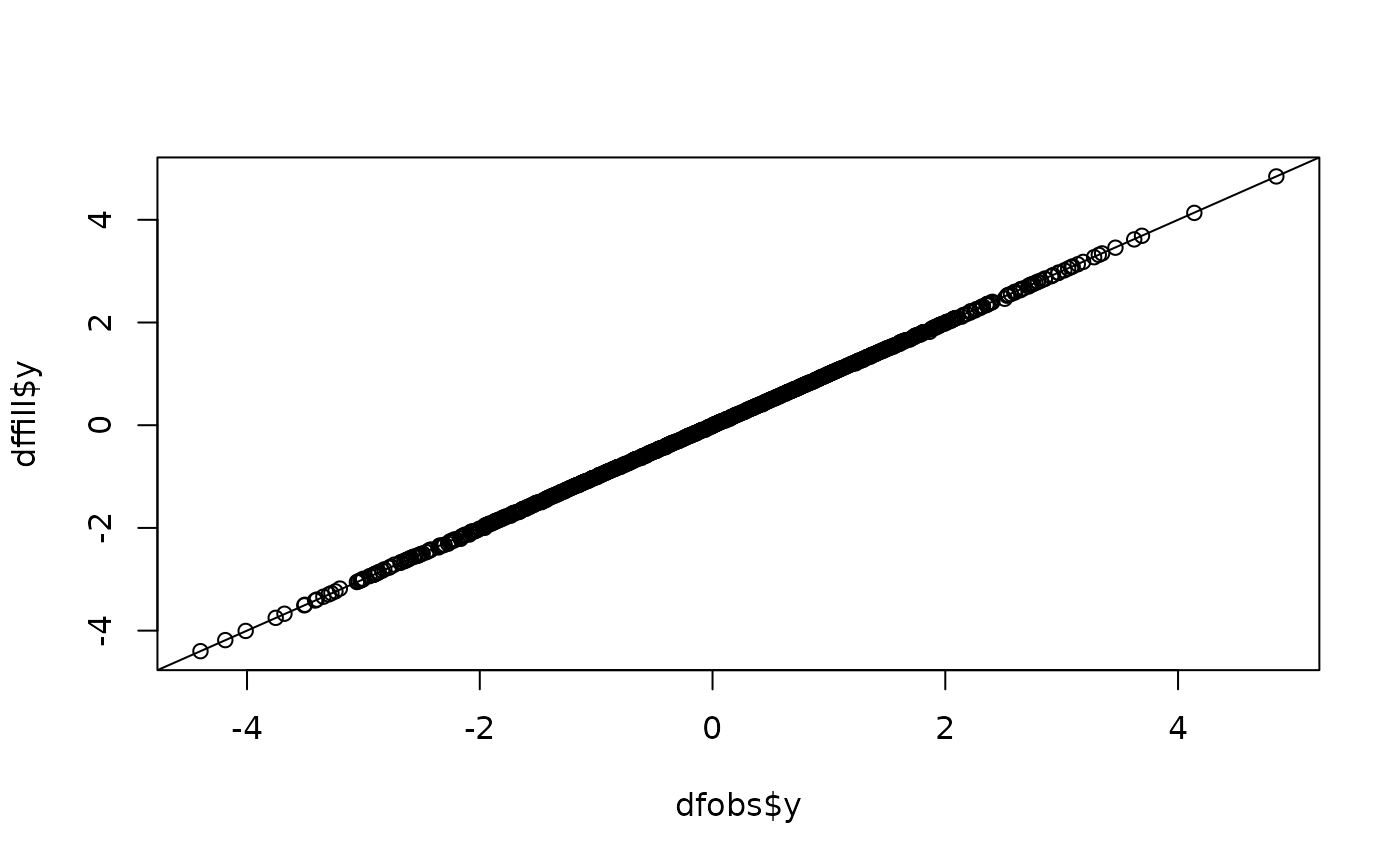
dffill2 <- generate(gpcavar,n=n,exogen=exogen,gap.filling=dfobs2,names=names(dfobs2)) 

qqplot(dfobs$y,dffill$y)
abline(0,1)

 
### generation with 'generetion.matrix' 
### and matrix 'x' is a covariance matrix 

covariance <- array(0.5,c(3,3))

diag(covariance) <- 1

set.seed(127)
ngns <- 1000
gg1 <- generate(FUN=rnorm,n=ngns,cov=covariance)
set.seed(127)
gg2 <- generate(covariance,type="covariance",n=ngns)


## generate with a list of covariance matrix 
ndim <- 5
dim <- c(ndim,ndim)
CS1 <- array(0.3,dim)
CS2 <- array(0.5,dim)
CS3 <- array(0.7,dim)
CS4 <- array(0.1,dim)

diag(CS1) <- 1
diag(CS2) <- 1
diag(CS3) <- 1
diag(CS4) <- 1

list <- list(CS1=CS1,CS2=CS2,CS3=CS3,CS4=CS4)

series <- rep(1:4,times=4,each=100)
series <- sprintf("CS%d",series)
names_A <- sprintf("A%d",1:ndim)
ggs <- generate(list,factor.series=series,FUN=rnorm,type="covariance",names=names_A)

ggs_CS1 <- ggs[series=="CS1",]
cov(ggs_CS1)
#>           A1        A2        A3        A4        A5
#> A1 0.9849989 0.3775549 0.3664686 0.3607563 0.3101554
#> A2 0.3775549 1.0670913 0.2906559 0.3528656 0.2713056
#> A3 0.3664686 0.2906559 1.0566839 0.3080295 0.4366083
#> A4 0.3607563 0.3528656 0.3080295 1.0739726 0.2584804
#> A5 0.3101554 0.2713056 0.4366083 0.2584804 1.0230544

ggs_CS3 <- ggs[series=="CS3",] 
cov(ggs_CS3)
#>           A1        A2        A3        A4        A5
#> A1 0.9013927 0.5579343 0.5757074 0.6085949 0.5956598
#> A2 0.5579343 0.9061509 0.5648254 0.6005457 0.6002669
#> A3 0.5757074 0.5648254 0.8507358 0.5574203 0.5934321
#> A4 0.6085949 0.6005457 0.5574203 0.8872049 0.6129122
#> A5 0.5956598 0.6002669 0.5934321 0.6129122 0.9216363

Arguments

Value

See also

Examples